GD&T for beginners: MMC & bonus tolerance, explained in 3D
ビギナーのための幾何公差:MMC(最大実体状態)とボーナス公差を3次元で解説
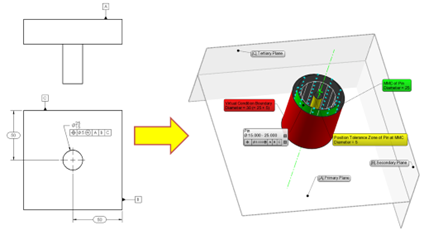
<図1>幾何公差:2次元対3次元
幾何公差の概念は、最初は理解するのが難しいため、初心者は基本原理を理解するのに非常に苦労します。この難しさの理由の一つは、2次元図面における3次元概念の視覚化です。
このブログ記事の目的は、ピン(シャフト)に対するMMC(最大実体状態)の概念を、簡単な例(図1)を用いて3次元的に分析することです。この例では、ASME Y14.5-2009規格の図2.15(33ページ)のケースを3次元で再現し、公差(および誤差)を大きくして分かりやすく視覚化しています。
▼最大実体状態(MMC)と最小実体状態(LMC): 簡単な定義
MMCとは、指定されたサイズの範囲内で、最小の穴または最大のピンを含む要素の状態をいいます。LMCとは、指定されたサイズの範囲内で、最大の穴または最小のピンの要素の状態をいいます。
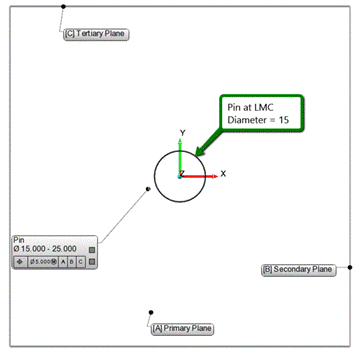
<図2>ピンのMMCとLMCのコンセプト
図2の例では、ピンのMMCは25mm、LMCは15mmを示しています。
▼MMCコンセプトを使う理由
MMCはワーストケースを定義しますが、その場合も部品が規定の公差の範囲内にあるため、ピンと穴の組み立ては保証されます。つまり穴が最小の状態(MMC)で、ピンが最大の状態(同じくMMC)であっても、その部品を組み立てることができます。このように、MMCはクリアランスのある組み合わせが一般的に広く使われています。
▼ボーナス公差のコンセプト
<図3>ボーナス公差の説明: ピンのサイズがMMCからLMCに向かうにつれて、そのずれ量に等しいボーナス公差が追加される。ボーナス公差は、実際の要素サイズと要素のMMCとの差に等しい。この場合、ボーナス公差=MMC-LMC=25-15=10となります。
相手要素の実際のサイズがMMCより小さい場合、組立のためのクリアランスは広くなります。ピンがMMCよりも小さく、LMCの限界に近い寸法で仕上げられた場合、得られたクリアランスは形状や位置のボーナス公差として使用することができます。この例では<図3>。
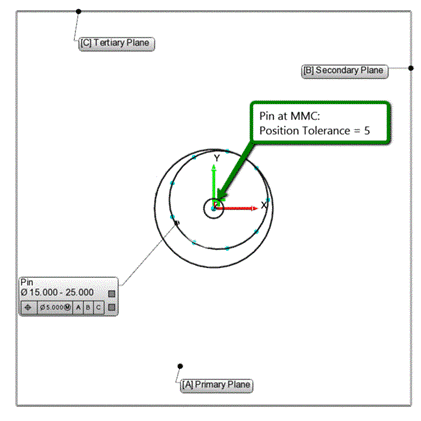
▼例1:MMCでのピンの直径
MMCでのピンの直径=25
ボーナス公差=0
MMCでの位置公差=5
MMCコンセプトとボーナス公差は3次元で見るともっと広くなる
1つ目ビデオでは、MMCのピンを表す円柱の中心軸が、直径5mmの円柱として定義された位置公差範囲で周っています。
▼例2:LMCでのピンの直径
LMCでのピンの直径=15
ボーナス公差=MMCのピンの直径-LMCのピンの直径=25-15=10
LMCの位置公差=5(MMCの公差)+10(ボーナス公差)=15
ピンはLMCに到達すると、より大きい位置公差幅を持ちます。
次の2つ目のビデオでは、LMCのピンを表す円柱の中心軸が、直径15mmの円柱として定義された位置公差範囲で周っています。今回はボーナス公差が大きいため、LMCでは許容される公差幅がより大きくなっています。
▼例3:中間の任意のピンの直径
ピンがLMCとMMCの間の任意の直径であると、何が起こるのでしょうか?
ピンの直径=20
ボーナス公差=MMCのピンの直径-ピンの直径=25-20=5
位置公差=5(MMCの公差)+5(ボーナス公差)=10
次の3つ目のビデオでは、任意の寸法のピンを表す円柱の中心軸が、直径10mmの円柱として定義された位置公差範囲で周っています。(この例では、ピンの直径は公称値ですが、必ずしもそうである必要はありません)
幾何公差および検査ワークフローを改善する方法について、詳しくはこちらのウェビナーをご覧ください(英語)。
――――――――――――――――――――――――――――――――――――――――
参考文献
ASME Y 14.5-2009 , Dimensioning and Tolerancing. New York: American Society of Mechanical Engineers.
【このページの関連ページ】
- 現場での3次元測定
- サイト内検索
- ページカテゴリ一覧
- 新着ページ
-
- お知らせ | オフィス(サポートセンター)移転のお知らせ (2026年02月09日)
- ニュースリリース | 新たな時代の幕開け: FAROとCreaformが統合し、2つの新しい事業部門を形成 (2026年02月04日)
- 【ハンディ3Dスキャナー】 Leap ST (2026年02月04日)
- 展示会 | TCT Japan (2026年01月27日)
- お知らせ | ファロージャパン本社電話番号変更のお知らせ (2026年01月19日)
- 動画 | Confidence You Can Measure ~信頼性の高い測定を~ (2025年12月18日)
- 展示会 | 建設技術フェア2025 in 中部 (2025年11月20日)
- 記事 | 幾何公差での平面度の評価方法 (2025年11月12日)
- 展示会 | ジャパンホームショー&ビルディングショー (2025年11月06日)
- ニュースリリース | FARO、Creaformとの連携によりHandySCAN BLACK|Eliteで3次元測定製品を拡大 (2025年10月30日)





![足で稼ぐ営業を見直しませんか?[営業支援サービスのご案内] 足で稼ぐ営業を見直しませんか?[営業支援サービスのご案内]](https://www.atengineer.com/pr/faro/color/images/btn_wps.png)